Exercise
Find the section in x-aixs where the line:
y=x+1
is below the parabla:
y=x^2-2x-9
Final Answer
Solution
We want to find for which points in x-aixs the following inequality is true:
x^2-2x-9>x+1
Move everything to one side:
x^2-2x-9-x-1>0
x^2-3x-10>0
It is a square inequality. Its coefficients are
a=1, b=-3, c=-10
The coefficient of the square expression (a) is positive, so the parabola (quadratic equation graph) “smiles” (= bowl-shaped). The sign of the inequality means we are looking for the sections the parabola is above the x-axis. We find the solutions (= zeros = roots) of the quadratic equation using the quadratic formula. Putting the coefficients in the formula gives us
x_{1,2}=\frac{3\pm \sqrt{{(-3)}^2-4\cdot 1\cdot (-10)}}{2\cdot 1}=
=\frac{3\pm \sqrt{49}}{2}=
=\frac{3\pm 7}{2}
Hence, we get the solutions:
x_1=\frac{3+ 7}{2}=5
x_2=\frac{3- 7}{2}=-2
Because the parabola we got “smiles” and we look for the section where it is above the x-axis, we get that the requested section is
x<-2 \text{ or } x>5
Here are the line and the parabola:
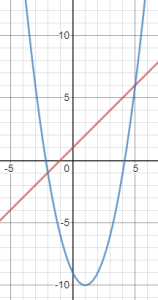
You can see that the line is indeed below the parabola in the section we found.
Have a question? Found a mistake? – Write a comment below!
Was it helpful? You can buy me a cup of coffee here, which will make me very happy and will help me upload more solutions!
