Exercise
Solve the square inequality:
6x-x^2<10
Final Answer
Solution
6x-x^2<10
Move everything to one side:
6x-x^2-10<0
It is a square inequality. its coefficients are:
a=-1, b=6, c=-10
The coefficient of the squared expression (a) is negative, so the parabola (quadratic equation graph) “cries” (= inverted-bowl-shaped). The sign of the inequality means we are looking for the sections the parabola is below the x-axis. We find the solutions (= zeros = roots) of the quadratic equation using the quadratic formula. Putting the coefficients in the formula gives us
x_{1,2}=\frac{-6\pm \sqrt{6^2-4\cdot (-1)\cdot (-10)}}{2\cdot (-1)}=
=\frac{-6\pm \sqrt{-6}}{-2}
We got a negative number inside the root, so there is no real solution to the quadratic equation, i.e. its graph does not pass through the x-axis. Because it is “crying”, it is always under the x-axis. Hence, inequality exists for every x.
The graph of the equation:
y=-x^2+6x-10
looks like this:
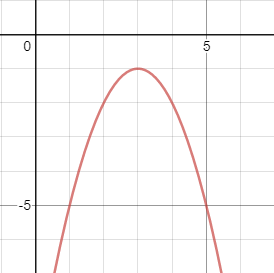
You can see that the graph is indeed below the x-axis for all x.
Have a question? Found a mistake? – Write a comment below!
Was it helpful? You can buy me a cup of coffee here, which will make me very happy and will help me upload more solutions!
