Exercise
Calculate the mass of T where T is bounded by the surfaces
y+z=1, 2y+z=2, x^2=2y
Given the density function
f(x,y,z)=y
Final Answer
Solution
Coming soon…
נמצא את המסה בעזרת אינטגרל משולש:
m=\int\int\int_T y dxdydz=
=\int dx\int dy\int y dz
נציב את גבולות האינטגרציה. ראשית, נבדוק מה קורה במישור XY. במישור מתקיים z=0. נציב זאת במשטחים ונקבל:
y+0=1\Longrightarrow y=1
2y+0=2\Longrightarrow y=1
נבודד את y במשטח השלישי, כדי שיהיה לנו קל לשרטט אותו:
x^2=2y\Longrightarrow y=\frac{x^2}{2}
נשרטט את הפונקציות שקיבלנו, כדי להבין איך התחום נראה במישור:
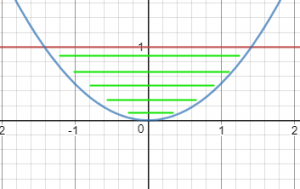
התחום מסומן בקווים ירוקים. כעת, יהיה לנו קל למצוא את גבולות האינטגרציה לפי x ולפי y. כדי למצוא את גבולות האינטגרציה, נעביר ישר המקביל לציר של משתנה האינטגרציה הפנימי. בExercise שלנו, נבחר את האינטגרל הפנימי להיות y, ולכן נעביר ישר המקביל לציר y. זה נראה כך:
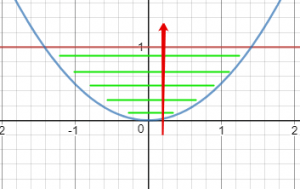
כעת, נבדוק לאיזה ערך y שווה כשנכנסים לתחום מלמטה ולאיזה ערך y שווה כשיוצאים מהתחום למעלה. אנו נכנסים לתחום בפרבולה:
y=\frac{x^2}{2}
ויוצאים מהתחום בישר:
y=1
נעבור למצוא את גבולות האינטגרציה החיצוניים (של האינטגרל השמאלי), לפי x. שימו לב שגבולות חיצוניים חייבים להיות קבועים, ללא המשתנים x,y או z. כדי למצוא את גבולות האינטגרציה החיצוניים, ניקח את הקטע הגדול ביותר בציר של משתנה האינטגרציה, החופף עם התחום במישור XY. לשם כך, נמצא את נקודות החיתוך בין הישר לפרבולה:
1=\frac{x^2}{2}
2=x^2
x=\pm\sqrt{2}
לכן, הקטע הגדול ביותר בציר x החופף לגוף T הוא
(-\sqrt{2},\sqrt{2})
נציב את גבולות האינטגרציה שקיבלנו:
m=\int_{-\sqrt{2}}^{\sqrt{2}} dx\int_{\frac{x^2}{2}}^1 dy\int y dz
נמצא את גבולות האינטגרציה לפי z. נבודד את z בשני המשטחים:
y+z=1\Longrightarrow z=1-y
2y+z=2\Longrightarrow z=2(1-y)
ואלה גבולות האינטגרציה לפי z. נציב אותם באינטגרל:
m=\int_{-\sqrt{2}}^{\sqrt{2}} dx\int_{\frac{x^2}{2}}^1 dy\int_{1-y}^{2(1-y)} y dz=
הערה: אם לא בטוחים איזו פונקציה צריכה להיות למטה ואיזו למעלה, מציבים נקודה והפונקציה בעלת הערך הנמוך יותר תהיה למטה, ובעלת הערך הגבוה – למעלה.
נפתור את האינטגרל. נתחיל כרגיל מהאינטגרל הפנימי (הימני ביותר) לפי z ונקבל:
=\int_{-\sqrt{2}}^{\sqrt{2}} dx\int_{\frac{x^2}{2}}^1 [yz]_{1-y}^{2(1-y)} dy=
נציב את גבולות האינטגרציה במקום z:
=\int_{-\sqrt{2}}^{\sqrt{2}} dx\int_{\frac{x^2}{2}}^1 [y\cdot 2(1-y)-y(1-y)] dy=
=\int_{-\sqrt{2}}^{\sqrt{2}} dx\int_{\frac{x^2}{2}}^1 [2y-2y^2-y+y^2] dy=
=\int_{-\sqrt{2}}^{\sqrt{2}} dx\int_{\frac{x^2}{2}}^1 (y-y^2) dy=
שוב, נפתור את האינטגרל הפנימי (הימני ביותר), הפעם לפי y, ונקבל:
=\int_{-\sqrt{2}}^{\sqrt{2}} [\frac{y^2}{2}-\frac{y^3}{3}]_{\frac{x^2}{2}}^1 dx=
נציב את גבולות האינטגרציה במקום y:
=\int_{-\sqrt{2}}^{\sqrt{2}} [\frac{1^2}{2}-\frac{1^3}{3}-(\frac{{(\frac{x^2}{2})}^2}{2}-\frac{{(\frac{x^2}{2})}^3}{3})] dx=
=\int_{-\sqrt{2}}^{\sqrt{2}} [\frac{1}{2}-\frac{1}{3}-(\frac{x^4}{8}-\frac{x^6}{24})] dx=
=\int_{-\sqrt{2}}^{\sqrt{2}} [\frac{1}{6}-\frac{x^4}{8}+\frac{x^6}{24}] dx=
הגענו לאינטגרל מסוים במשתנה אחד – x. נפתור אותו:
=[\frac{1}{6}x-\frac{x^5}{8\cdot 5}+\frac{x^7}{24\cdot 7}]_{-\sqrt{2}}^{\sqrt{2}}=
נציב את גבולות האינטגרציה:
=\frac{1}{6}\sqrt{2}-\frac{{(\sqrt{2})}^5}{8\cdot 5}+\frac{{(\sqrt{2})}^7}{24\cdot 7}-(\frac{1}{6}\cdot (-\sqrt{2})-\frac{{(-\sqrt{2})}^5}{8\cdot 5}+\frac{{(-\sqrt{2})}^7}{24\cdot 7})=
=\frac{1}{6}\sqrt{2}-\frac{{(\sqrt{2})}^5}{40}+\frac{{(\sqrt{2})}^7}{168}+\frac{1}{6}\sqrt{2}-\frac{{(\sqrt{2})}^5}{40}+\frac{{(\sqrt{2})}^7}{168}=
=\frac{1}{3}\sqrt{2}-\frac{8\sqrt{2}}{40}+\frac{16\sqrt{2}}{168}=
=\frac{8}{35}\sqrt{2}
הערה: אפשר לפתור את האינטגרל בסדר אינטגרציה שונה, למשל dzdydx או כל סדר אחר, אבל גבולות האינטגרציה ישתנו בהתאם. את רוב התרגילים יהיה הכי פשוט וקל לפתור בסדר האינטגרציה הרגיל dxdydz, כמו בExercise הזה.
עזרתי לך להבין את החומר? אשמח לתרומה צנועה של כוס קפה כאן, כדי שאוכל להעלות בכיף פתרונות נוספים 🙂
רוצה פתרונות נוספים בנושא זה או בנושאים אחרים? – ספר/י לי כאן ואשמח לעזור.
מצאת טעות? יש לך שאלה בנוגע לפתרון זה? השאיר/י תגובה למטה ואשמח לענות.
[\hide]
