Exercise
Find the area of the region bounded by the graphs of the equations:
y=6-x^2, y=x^2-2x-6
Final Answer
Solution
First, we find out how the area looks like:
6-x^2=x^2-2x-6
2x^2-2x-12=0
(x+2)(x-3)=0
x=-2, x=3
The area looks like this:
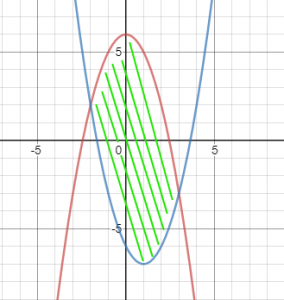
S=\int_{-2}^3 6-x^2-(x^2-2x-6) dx=
=\int_{-2}^3 -2x^2+2x+12 dx=
=[-2\cdot\frac{x^3}{3}+2\cdot\frac{x^2}{2}+12x]_{-2}^3=
=[-2\cdot\frac{x^3}{3}+x^2+12x]_{-2}^3=
=-2\cdot\frac{3^3}{3}+3^2+12\cdot 3-(-2\cdot\frac{{(-2)}^3}{3}+{(-2)}^2+12\cdot (-2))=
=-18+9+36-\frac{16}{3}-4+24=
=27+14\frac{2}{3}=
=41\frac{2}{3}
Have a question? Found a mistake? – Write a comment below!
Was it helpful? You can buy me a cup of coffee here, which will make me very happy and will help me upload more solutions!
