Domain of One Variable Function – A function with square root – Exercise 5738

Exercise

Determine the domain of the function:

$y=\sqrt{3x-x^3}$

Final Answer

Show final answer

Solution

Let’s find the domain of the function:

$y=\sqrt{3x-x^3}$

Because there is a square root, the expression inside the root must be non-negative:

$3x-x^3\geq 0$

Let’s find the roots of the polynomial equation:

$3x-x^3=0$

Factor the polynom:

$x(3-x^2)=0$

$x(x-\sqrt{3})(x+\sqrt{3})=0$

Therefore, its roots are

$x=0,\pm\sqrt{3}$

We are interested in the domain that holds this inequality:

$x(x-\sqrt{3})(x+\sqrt{3})\geq 0$

Therefore, the solution is

$x\leq -\sqrt{3}\text{  or  } 0\leq x\leq \sqrt{3}$

The polynom:

$y=3x-x^3$

looks like this:

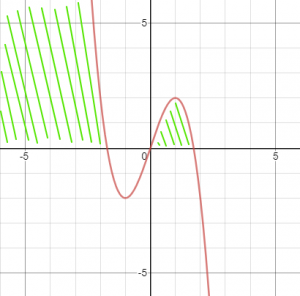
The domain is marked in green lines.

Have a question? Found a mistake? – Write a comment below!
Was it helpful? You can buy me a cup of coffee here, which will make me very happy and will help me upload more solutions!