Exercise
Determine the domain of the function:
f(x)=\sqrt[4]{\log_2 (\tan x)}
Final Answer
Solution
Let’s find the domain of the function:
f(x)=\sqrt[4]{\log_2 (\tan x)}
Because there is a log, we need the expression inside the log to be greater than zero:
\tan x >0
Also, there is a fourth root, so we need the expression inside the root to be non-negative:
\log_2 (\tan x)\geq 0
First, we solve the second inequality. Because the log base is greater than one (2), By logarithm laws one get:
2^{\log_2 (\tan x)}\geq 2^0
\tan x\geq 1
We look for the domain in the x-axis in which the following holds:
\tan x\geq 1\text{ and }\tan x >0
Together we get that the function domain is when the following holds:
\tan x\geq 1
Tan function looks like this:
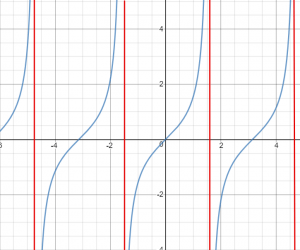
The tan function (marked in blue) is a pie-length cyclic function that continues in a similar manner from minus infinity to infinity. Notice that it has infinite vertical asymptotes (marked in red) at the points:
x=\frac{\pi}{2}+k\pi, k\in Z
Let’s check when the following holds:
\tan x= 1
The function equals 1 at the points:
x=\frac{\pi}{4}+k\pi, k\in Z
Each cycle (between any two asymptotes) has the same ascending monotone function. Therefore, the domain we are looking for is the domain in the x-axis from the point where the function equals one (including that point) to the end of the continuous segment (until the next asymptote, and therefore without the end point). Hence, the function domain is
\cup_{k=-\infty}^{k=\infty} [\frac{\pi}{4}+k\pi,\frac{\pi}{2}+k\pi)=
=... \text{ and }[-\frac{3\pi}{4},-\frac{\pi}{2})\text{ and }[\frac{\pi}{4},\frac{\pi}{2}) \text{ and }[\frac{5\pi}{4},\frac{3\pi}{2}) \text{ and }...
Have a question? Found a mistake? – Write a comment below!
Was it helpful? You can buy me a cup of coffee here, which will make me very happy and will help me upload more solutions!
